★ Вяткин Артем Андреевич ★

Оценка и применение третичной структуры АБС в апостериорном выводе

• ПОБЕДИТЕЛЬ

  в рейтинге студентов лаборатории ТиМПИ

• 3 курс

  МАТОБЕС

• Тулупьев Александр Львович

  Научный руководитель​

• Харитонов Никита Алексеевич

  Куратор​

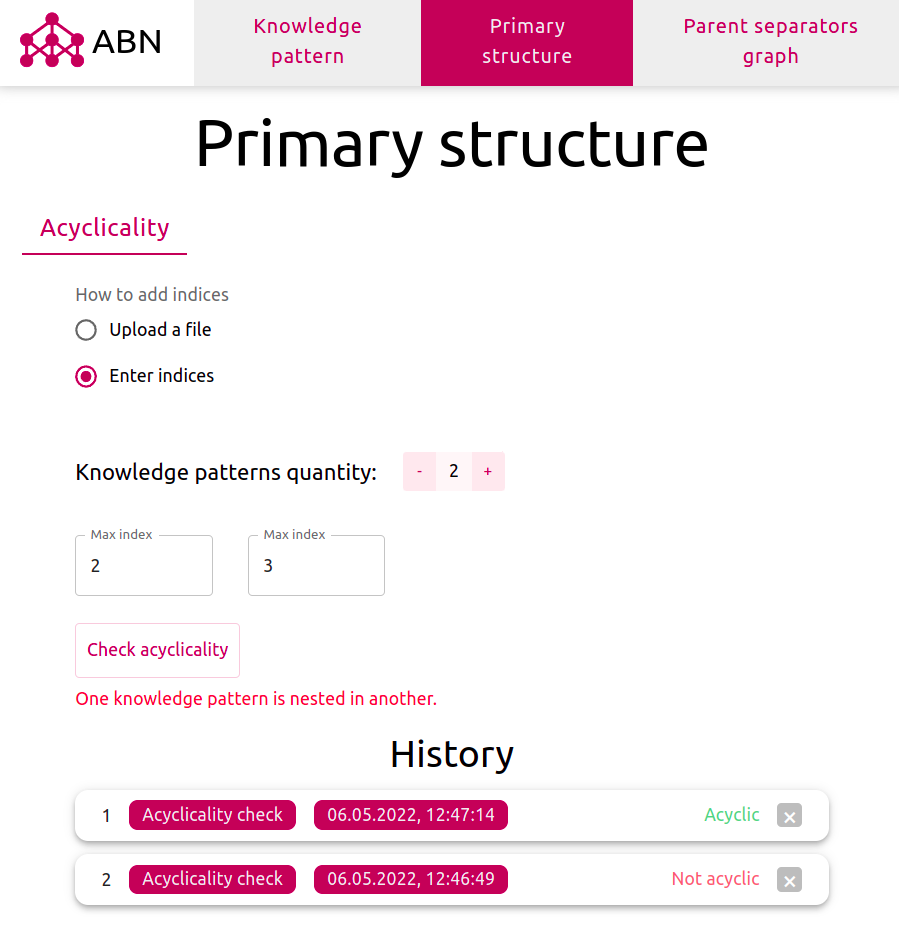
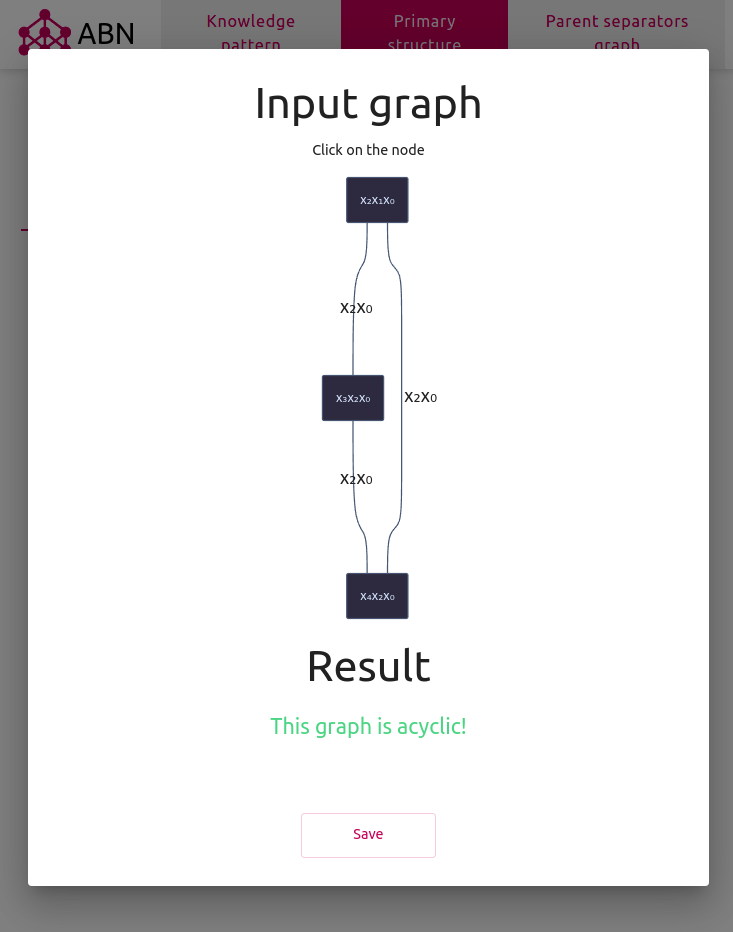
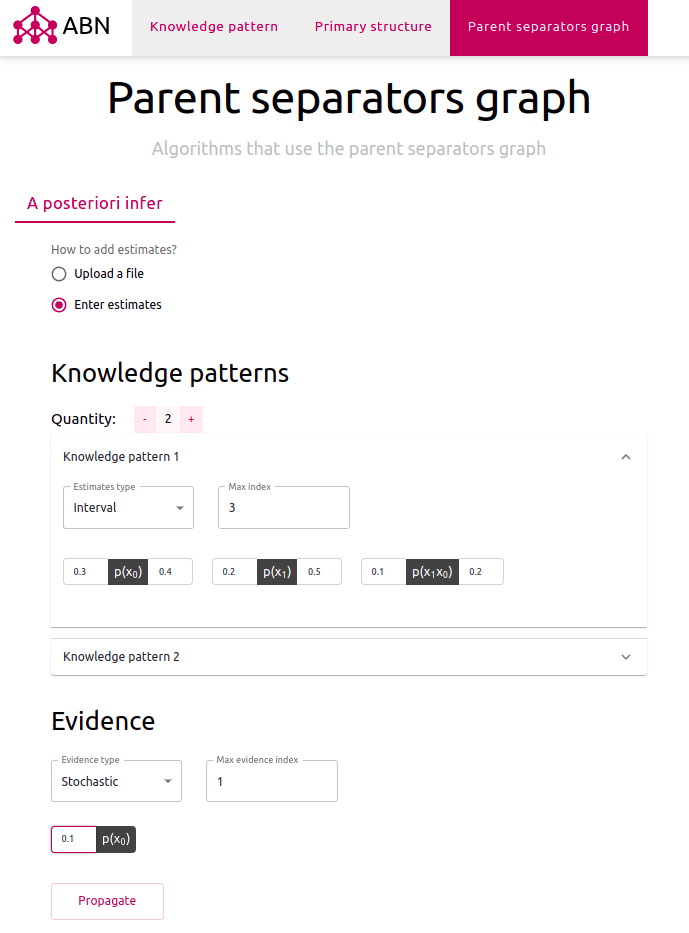
«Глобальная задача — описать математическую модель для работы с утверждениями и вероятностями их истинности. В роли таких моделей могут выступать алгебраические байесовские сети (АБС). Базовой структурой в этих сетях является математическая модель фрагмента знаний, которая наиболее полно описывает взаимосвязи между небольшим набором утверждений. Над наборами фрагментов знаний строятся более обширные структуры — первичная, вторичная, третичная. Последние две из них — графы с фрагментами знаний как нагрузками вершин. Такие структуры вместе с изначально заданными оценками вероятности истинности отдельных элементов могут быть противоречивыми. Так же необходимо проводить глобальный апостериорный вывод — обработку поступления новой информации, представленной в виде свидетельства. В частности, такая обработка заключается в распространении свидетельства, то есть пересчете оценок. Вернемся к моей работе. Глобальный апостериорный вывод на текущий момент проводится с применением вторичных структур, для построения которых использовались третичные. Можно ли, и, если можно, то как использовать только третичную структуру для проведения такого вывода? Цель моей работы и заключалась в ответах на эти вопросы, а так же на вопрос проверки непротиворечивости АБС с применением третичной структуры. В результате были составлены и автоматизированы соответствующие алгоритмы, проведена оценка их вычислительной сложности. Работу этих алгоритмов можно посмотреть на сайте https://abn.dscs.pro/. В будущем планируется более детально сравнить полученные алгоритмы и алгоритмы, использующие вторичную структуру.» Артем Андреевич Вяткин Рекомендуемая Артёмом Андреевичем литература для погружения в теорию алгебраический байесовских сетей: 1. Начальное ознакомление с теорией АБС: Тулупьев А. Л. Алгебраические байесовские сети: локальный логико-вероятностный вывод: Учеб. пособие // СПб.: ООО Издательство «Анатолия», 2007. 80 c. 2. Знакомство со вторичной структурой, глобальным выводом: Тулупьев А. Л. Алгебраические байесовские сети: глобальный логико-вероятностный вывод в деревьях смежности. // СПб.: ООО Издательство «Анатолия», 2007. 3. Более подробное знакомство с алгориматми и структурами, в частности, третичной: Фильченков А. А. Синтез графов смежности в машинном обучении глобальных структур алгебраических байесовских сетей: Диссертация на соискание ученой степени кандидата физико-математических наук. СПб., 2013. 339 с. (Санкт-Петербургский государственный университет.)